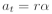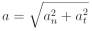Biomechanika - studijní materiály

Pohyb bodu po kružnici

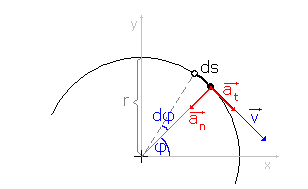
Poloha bodu při pohybu po kružnici lze určit pomocí poloměru kružnice r a úhlu φ, který svírá průvodič bodu (spojnice bodu se středem kružnice) a osa x. Poloměr kružnice r je konstantní, zatímco velikost úhlu φ je funkcí času.

Dráha pohybu po kružnici

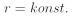
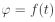
Bod pohybující se po kružnici urazí za určitý časový okamžik dt dráhu ds po obvodu této kružnice, přičemž průvodič tohoto bodu opíše úhel dφ. Mezi dráhou ds a úhlem dφ platí vztah:

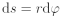
jinými slovy, posun bodu o dráhu ds po kružnici je provázen změnou úhlu dφ.

Rychlost bodu při pohybu po kružnici

Při pohybu bodu po kružnici se rozlišují dvě veličiny: rychlost a úhlová rychlost. U obou veličin se pak může vyšetřovat jak okamžitá, tak průměrná hodnota. Průměrná rychlost udává jakou dráhu urazil bod po obvodu kružnice v určitém časovém intervalu, zatímco průměrná úhlová rychlost udává jak velký úhel opsal průvodič bodu během tohoto časovém intervalu. Při pohybu bodu po kružnici směřuje vektor rychlosti daného bodu vždy ve směru tečny ke kružnici, po níž se bod pohybuje. Obecně platí, že vektor rychlosti bodu je vždy tečný k trajektorii bodu.

Okamžitá rychlost:

Okamžitá úhlová rychlost:

Vztah mezi rychlostí a úhlovou rychlostí:

Zrychlení bodu při pohybu po kružnici

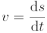
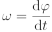
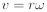
Narozdíl od pohybu bodu po přímce, kdy je uvažována pouze jedna složka zrychlení daného bodu, jsou při pohybu bodu po kružnici vždy uvažovány dvě složky zrychlení tohoto bodu a to tečné a normálové (dostředivé) zrychlení. Normálová složka zrychlení způsobuje změnu směru vektoru rychlosti daného bodu, zatímco tečná složka zrychlení způsobuje změnu velikosti vektoru rychlosti. Vzhledem k tomu, že vektor rychlosti směřuje vždy ve směru tečny ke své trajektorii, se směr vektoru rychlosti při pohybu po kružnici neustále mění. Z toho vyplývá, že normálová složka zrychlení, která tuto změnu způsobuje, je vždy nenulová. V případě, že je normálová složka zrychlení nulová, se bod pohybuje po přímce. Normálové zrychlení směřuje vždy do středu kružnice (resp. středu křivosti trajektorie bodu). V případě, že nedochází ke změně velikosti vektoru rychlosti, je tečná složka zrychlení nulová.

Normálové (dostředivé) zrychlení:

Změna úhlové rychlosti je vyjádřena úhlovým zrychlením α.

Tečné zrychlení charakterizuje změnu velikosti rychlosti, je tedy dáno vztahem:

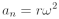
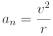
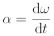
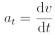
Po dosazení lze tento vztah zapsat následovně:

Výsledný vektor celkového zrychlení lze získat vektorovým součtem normálového a tečného zrychlení. Jeho velikost se vypočte pomocí Pythagorovy věty: