Výpočtové systémy - OptiSLang

Testovací úloha

Zadání

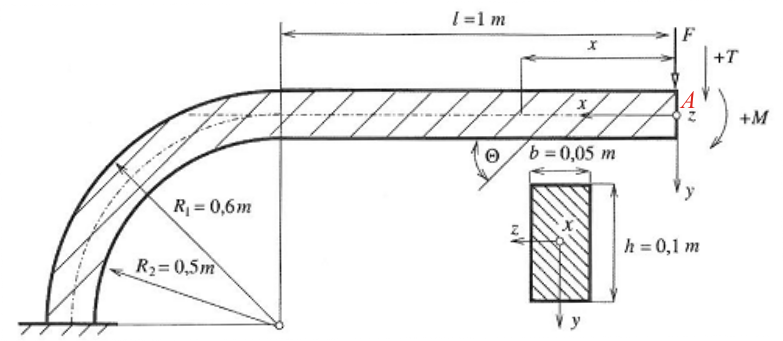
Práci s programem OptiSLang si ukážeme na jednoduché úloze. Na obrázku je znázorněn vetknutý křivý prut vyrobený z jednosměrové laminy a na konci zatížený silou \(F = 1000 \text{N} \). Materiálové konstanty laminy jsou \(E_1 = 87 \ \text{GPa} \), \(E_2 = 5,5 \ \text{GPa} \), \(G_{12} = 2,2 \ \text{GPa} \) a \(\nu_{12} = 0.34 \). Určete pro který úhel orientace vláken \( {\it\Theta} \) je průhyb \(y(A)\) pod silou \( F\) minimální.

Řešení

Úlohu musíme přeformulovat do tvaru optimalizační funkce:

\( \min\limits_{{\it\Theta}} f({\it\Theta}) = y(A) \) \(-90 \leqq \theta \leqq 90 \),

(1)

kde \( f({\it\Theta}) \) je cílová funkce vyjadřující průhyb v bodě \( A \) a úhel orientace laminy \( \it\Theta \) je optimalizační proměnná.

Vyčíslení cílové funkce provedeme metodou konečných prvků v programu MSC.Marc pro úhel \( {\it\Theta}~=~45° \). Sestavení modelu, provedení výpočtu a uložení výsledků je ukázáno v animaci 1. Soubor .proc pro sestavení modelu je ke stažení zde pasek_modelovani.proc a .proc soubor pro tištění výsledků je ke stažení zde pasek_vyhodnot.proc. Optimalizaci provedeme v programu OptiSlang v dále.